Some months ago, I came up with a little joking idea: what if, instead of hexagonal or square bins, cartographers used Penrose tiles?
A Penrose tiling is a form of tessellation. It’s fun and unique in that it fills the entire plane, but has no repeats. Wikipedia has more detail about how these things are cool. Mostly, I thought of them because they look interesting and are sort of regular, without being too regular.
So for fun, I made a couple of maps using Penrose bins.
![Density [Converted]-01](https://somethingaboutmaps.files.wordpress.com/2015/04/density-converted-01.png?w=1024&h=745)
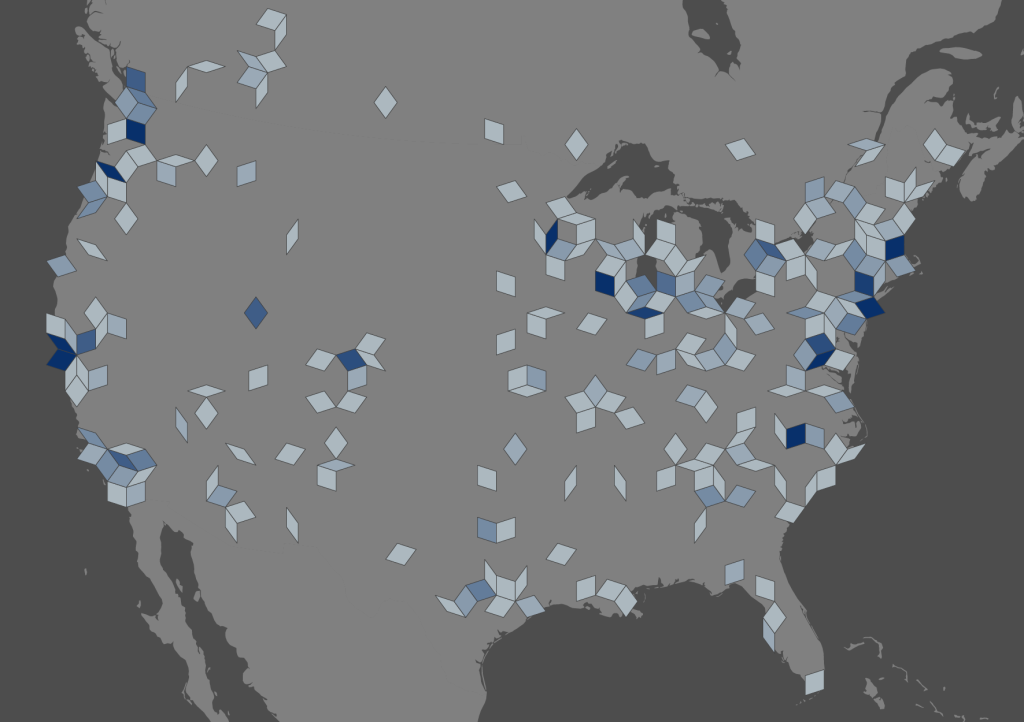
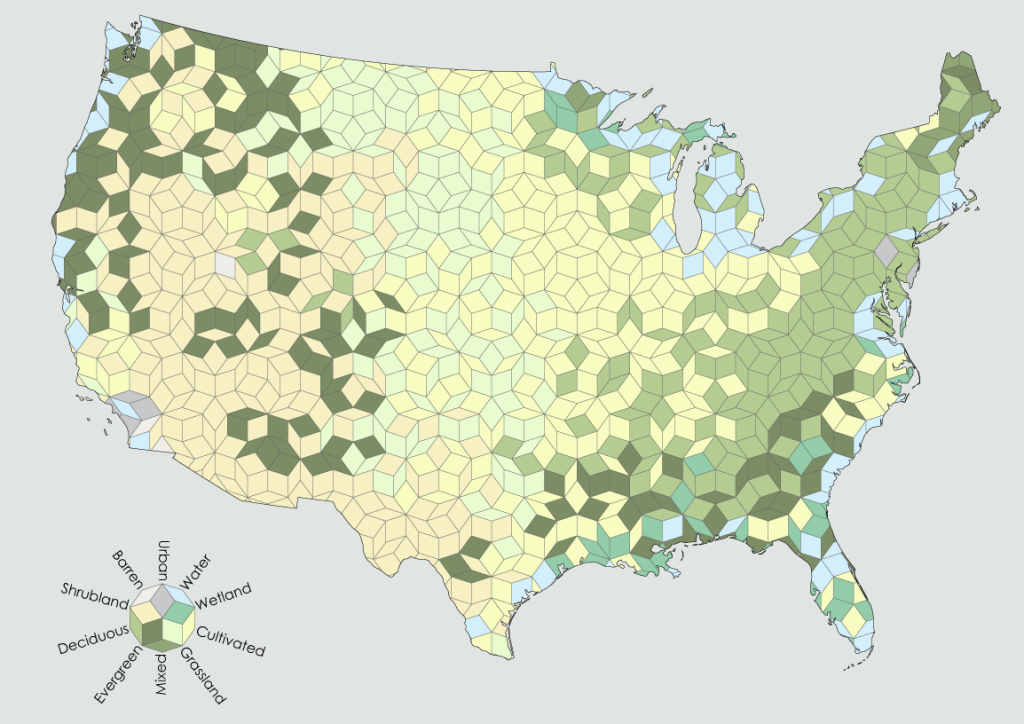
I can think of no proper cartographic use for Penrose binning, but it’s fun to look at, and so that’s good enough for me.
To create the tiles, I found an SVG of a Penrose tiling here: http://faa.hu/new/english/parquet1/index.php. Then I pulled it into QGIS and resized it to fit appropriately on the US and part of Canada when in an Albers Equal Area conic (CM: -96º, SP1: 20º, SP 2: 60º). Then I did zonal statistics in ArcMap (for population density and land cover) or a spatial join in QGIS (for the point data of Atlas of Design sales).
If you want to give it a try yourself, I’ve put the shapefile here: https://www.dropbox.com/s/soakfi8z5cp7by6/Penrose%20Tiles.zip?dl=0.
While I can’t think of a use for this presently, who knows what the future will hold? Silly little experiments like this sometimes become valuable later on.
That is far to beautiful to be a map (:
If the tiling were done algorithmically (computationally expensive though it may be), an advantage of this system would be that it could better approximate shape outlines than is possible with hexagons or squares, and possibly equilateral triangles.